Hi, I’m Nick Derr!

This is me

I model and study systems in physics and biology. I was a postdoctoral instructor at MIT Math. I completed my PhD at Harvard, where I was advised by Chris Rycroft. Before that, I majored in Applied Math, Engineering and Physics at the University of Wisconsin and did Part III Maths at Cambridge University. I enjoy long-distance running, crossword puzzles and old paperbacks.

My PhD research focused on modeling systems with elements of fluid–structure interaction, including eroding porous media and simple swimmers. I also developed high-performance computational methods for similar settings, such as suspensions of soft immersed bodies and active gels.

Download my CV here. Read more about me here. Below are some short summaries of my research and publications.

My email is nicholas dot derr at gmail dot com. Thanks for visiting!

Research

My research centers on interactions between fluid and solid aspects of systems, often in porous, deforming systems arising in biological contexts. Here are a few of my past and present projects.

Erosion dynamics

Branching patterns can be seen in nature in a wide variety of contexts, from small biological systems (venation systems) to large geophysical settings (river systems.) A simple mechanical model for erosion is capable of producing branching patterns such as these. (PRL, arXiv)

Branching patterns

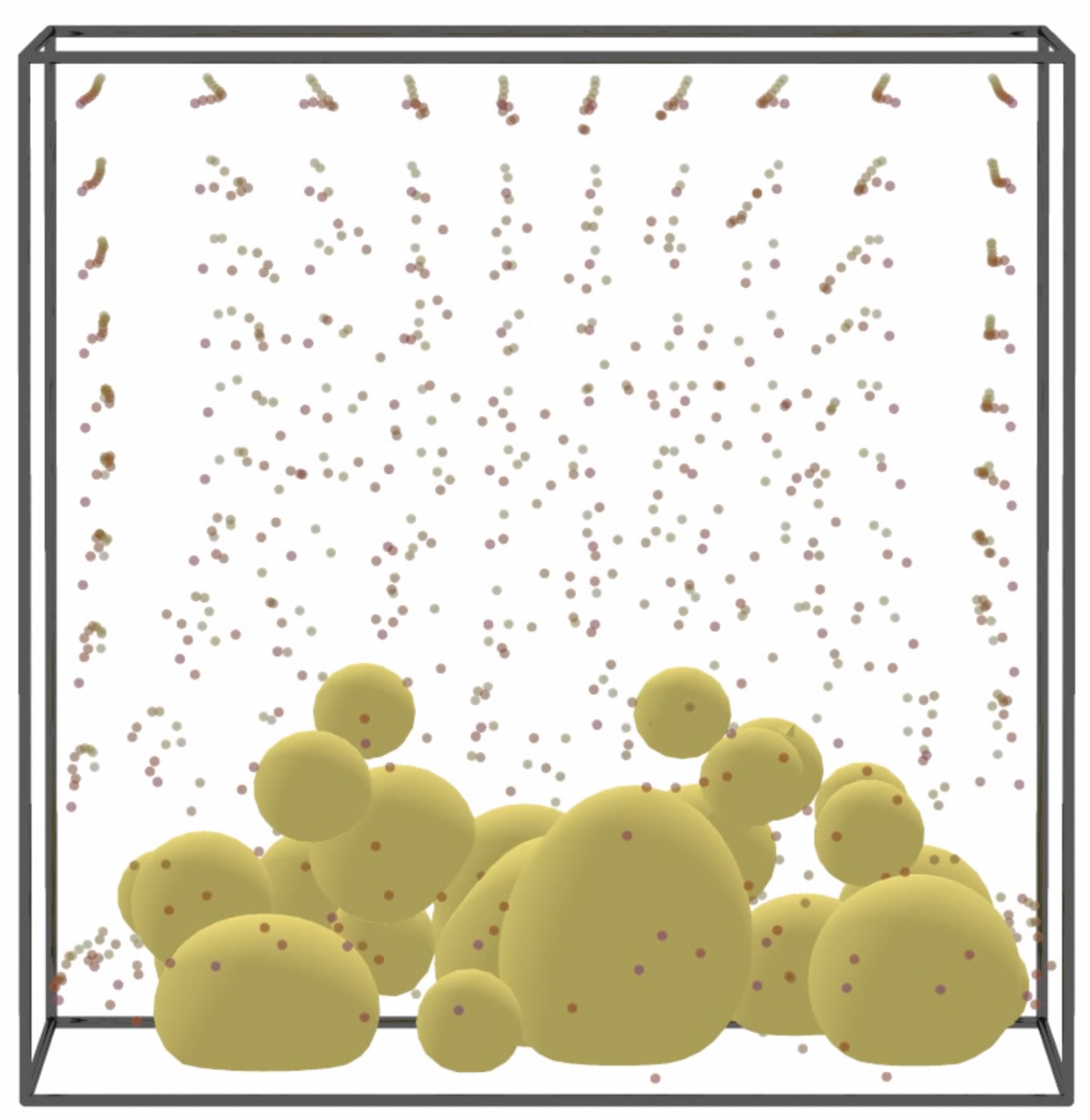
Reference map methods

The reference map technique is a fully Eulerian technique for the coupled simulation of immersed soft solid bodies in fluid. In three dimensions, the technique is well-suited for the simulation of many interacting bodies, such as the setting spheres shown here, or active solids. (PNAS, arXiv).

Settling soft spheres

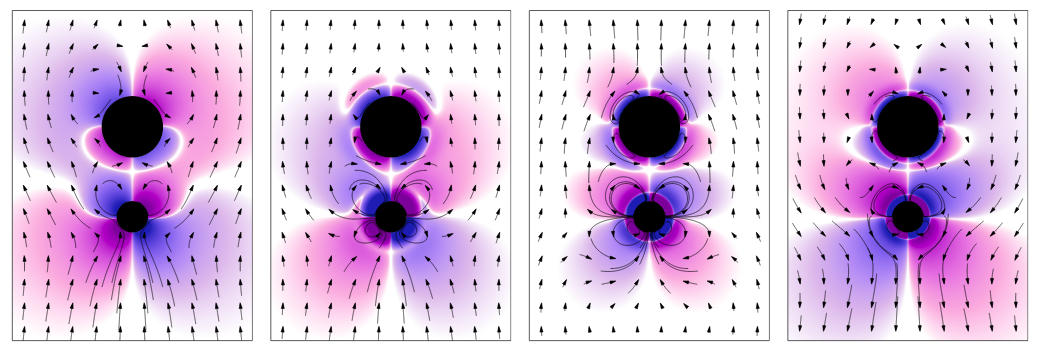
Reciprocal swimmers

In extremely viscous flow, inertia is unimportant. Purcell’s scallop theorem states that swimmers in such settings with time-reversible (“reciprocal”) strokes don’t move over time. An asymmetric dimer with oscillating length is a simple example of such a swimmer. A general model for the steady flow field generated by small-amplitude actuation unifies several previous results, including motion of a dense dimer in Stokes flow and a dimer in inertial flow. The latter, shown below, displays interesting dynamics where the direction of motion flips from towards the small sphere (left) to the large sphere (right) as the flow’s degree of inertia increases. (arXiv).

Steady flow fields

Cytoskeletal gels

Our cells’ interiors consist of a complex network of polymer filaments. This porous medium is subject to active stresses imparted by mechanical motor proteins. Experimental results show actin networks actuated by myosin proteins display a wide range of behaviors. Our model of the system, coupling active tension to motor binding dynamics, show behavior that may be reminiscent of thermodynamic phase separation (bottom right) or novel (top left) depending on system parameters.

Gel patterns

Preprints and Selected Publications

  1. N.J. Derr and C.H. Rycroft. A projection method for porous media flow, current draft (2022).
  2. N.J. Derr, T. Dombrowski, C.H. Rycroft, and D. Klotsa. Reciprocal swimming at intermediate Reynolds number. Journal of Fluid Mechanics 952, A8 (2022). [arXiv]
  3. Y.L. Lin, N.J. Derr, and C.H. Rycroft. Eulerian simulation of complex suspensions and biolocomotion in three dimensions. Proceedings of the National Academy of Sciences 119, e2105338118 (2021). [arXiv]
  4. N.J. Derr*, D.C. Fronk*, C.A. Weber, A. Mahadevan, C.H. Rycroft, and L. Mahadevan. Flow-driven branching in a frangible porous medium. Physical Review Letters 125, 158002 (2020). [arXiv]

Asterisks denote equal contribution.